jdc
Well-known member
I've trying to work out the drag on my boat while driving it through the water. Doubtless standard stuff for naval architects armed with 3D CAD programs and tank models like there are at the Wolfson unit in Southampton, but the data seems never to be released by boat builders or designers.
I think I now have some rather simple approximations which nonetheless give quite good results. Any naval architects out there who can comment?
My primary purpose was to work out what my fuel consumption would be, but for added spice I've contrived to subvert it into an anchoring related topic as well! Again, I'd actually be interested in actual data confirming or contradicting the results.
Underlying Theory
The drag is due to both friction, aka viscous forces, and to wave generating resistance. After some reading of papers (in particular a shamefully treated Australian called Mitchell seems to have done the fundamental work in this area), and trying to digest "Practical Ship Hydrodynamics" by Volker Bertram, I think that these are reasonable approximations:
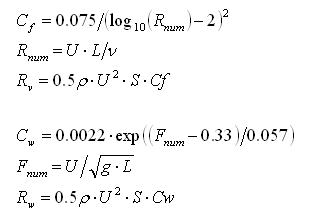

The formula and parameters in the wave drag equation are an empirical fit I made to the Mitchell triple integral, see figure 2 from this paper: http://journals.cambridge.org/downl...29a.pdf&code=3b0d45f2a0482099a22b52fd9ff5084a . The viscous drag is a standard result referenced all over the place.
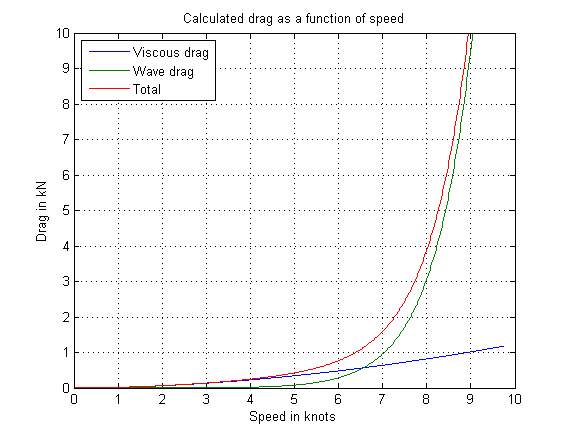
For my boat, 42' monohull with longish keel and rather traditional shape, they give drag like this:
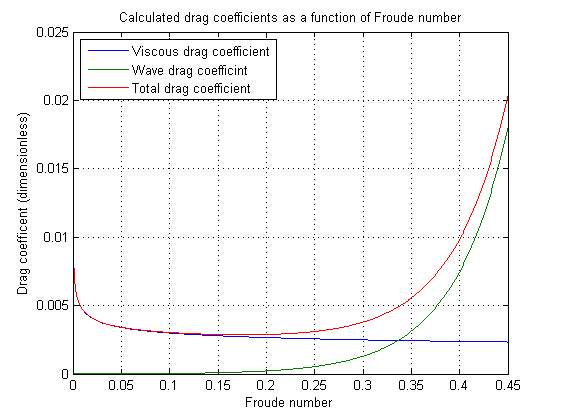
or, normalising to just the coefficients, which are likely applicable to other people's monohulls.
Actually I found the forces quite surprisingly low - so has anyone got measured data, eg from towing real boats?
What certainly stands out is why I can rather quickly get to 7 kts or so under sail, but getting above 9 takes some doing.
Range Under Power
Now we have drag related to speed, it can also be related to engine rpm knowing the prop pitch and diameter and making an assumption about efficiency. I chose 60% at full revs, which is quite low but I think my Gori 3 blade is not terribly efficient.
I couldn't find any useful equations relating thrust to shaft rpm in the literature: plenty for airscrews but not for water. So after some thought I tentatively used:
R = alpha * (beta * rpm - U);
R is the thrust,
U is the speed through the water
beta is related to pitch, and
alpha is related to diameter and water density.
This seems intuitively correct, but anyone know a more sophisticated one?
The result is plotted here. The red 'x's are values of speed vs rpm I measured last weekend, and the blue line is what the model predicts; I was rather pleased with the fit.

Also plotted is engine fuel consumption in miles per litre and thus range given a 300 litre tank. If true, this really does say that generally we motor too fast - up 'til now I've done between 1800 and 2000 rpm, but it's clear that 1200 - 1400 would be much more economical.
To convert from thrust to shaft HP I again had to make up the relationship, proposing
HP = gamma * rpm * ((beta * rpm - U) + epsilon);
gamma is a simple scaling factor I should be able to work out exactly, and is not worrying
epsilon is there to account for the losses of the real propeller, chosen to make it 60% efficient at full power.
To try to get some extra validation I also plotted HP and the calculated fuel consumption in litres per hour. The red 'x's are the values given by the Beta 50HP data sheet:

The fit is quite good; certainly the shape is spot-on, and if I find the data sheet a bit optimistic that's in accordance with my observation.
Subverting the thread to Anchoring
Since we already know how to relate horizontal force on a boat to wind speed, and we now can relate drag on the hull to speed through the water, we can calculate the effective increase in wind speed that a tide will give. This is plotted below. No dependency on anchor type or scope etc, so I hope not controversial in principle.
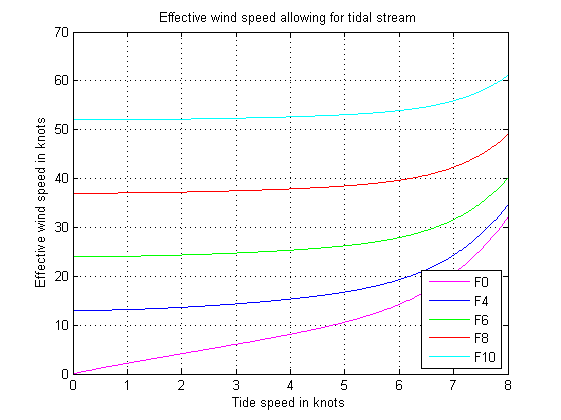
I was surprised at how small an effect the tide has if aligned with the wind. My conclusion is that the undoubted effect of tide when at anchor is much more to do with the sheering, and thus dynamic forces it creates, than due to a simple increase in static load. Not exactly an earth-shattering conclusion.
The last thing I bothered plotting was the bollard pull I'd get, when motoring in reverse. This is less than the forward pull due to the different gear ratio, but in my case of a Gori not to do with propeller shape since it's symmetrical between forward and reverse.
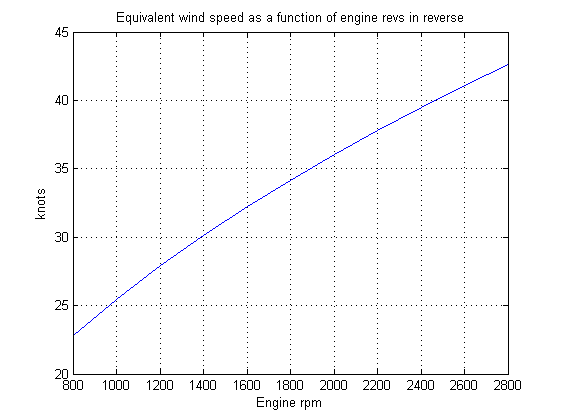
It should tell me how many revs to apply when making sure my anchor is well dug in.
Working this out amused me for a few mins on a Friday lunchtime anyway. Have a good weekend.
I think I now have some rather simple approximations which nonetheless give quite good results. Any naval architects out there who can comment?
My primary purpose was to work out what my fuel consumption would be, but for added spice I've contrived to subvert it into an anchoring related topic as well! Again, I'd actually be interested in actual data confirming or contradicting the results.
Underlying Theory
The drag is due to both friction, aka viscous forces, and to wave generating resistance. After some reading of papers (in particular a shamefully treated Australian called Mitchell seems to have done the fundamental work in this area), and trying to digest "Practical Ship Hydrodynamics" by Volker Bertram, I think that these are reasonable approximations:
The formula and parameters in the wave drag equation are an empirical fit I made to the Mitchell triple integral, see figure 2 from this paper: http://journals.cambridge.org/downl...29a.pdf&code=3b0d45f2a0482099a22b52fd9ff5084a . The viscous drag is a standard result referenced all over the place.
For my boat, 42' monohull with longish keel and rather traditional shape, they give drag like this:

or, normalising to just the coefficients, which are likely applicable to other people's monohulls.

Actually I found the forces quite surprisingly low - so has anyone got measured data, eg from towing real boats?
What certainly stands out is why I can rather quickly get to 7 kts or so under sail, but getting above 9 takes some doing.
Range Under Power
Now we have drag related to speed, it can also be related to engine rpm knowing the prop pitch and diameter and making an assumption about efficiency. I chose 60% at full revs, which is quite low but I think my Gori 3 blade is not terribly efficient.
I couldn't find any useful equations relating thrust to shaft rpm in the literature: plenty for airscrews but not for water. So after some thought I tentatively used:
R = alpha * (beta * rpm - U);
R is the thrust,
U is the speed through the water
beta is related to pitch, and
alpha is related to diameter and water density.
This seems intuitively correct, but anyone know a more sophisticated one?
The result is plotted here. The red 'x's are values of speed vs rpm I measured last weekend, and the blue line is what the model predicts; I was rather pleased with the fit.

Also plotted is engine fuel consumption in miles per litre and thus range given a 300 litre tank. If true, this really does say that generally we motor too fast - up 'til now I've done between 1800 and 2000 rpm, but it's clear that 1200 - 1400 would be much more economical.
To convert from thrust to shaft HP I again had to make up the relationship, proposing
HP = gamma * rpm * ((beta * rpm - U) + epsilon);
gamma is a simple scaling factor I should be able to work out exactly, and is not worrying
epsilon is there to account for the losses of the real propeller, chosen to make it 60% efficient at full power.
To try to get some extra validation I also plotted HP and the calculated fuel consumption in litres per hour. The red 'x's are the values given by the Beta 50HP data sheet:

The fit is quite good; certainly the shape is spot-on, and if I find the data sheet a bit optimistic that's in accordance with my observation.
Subverting the thread to Anchoring
Since we already know how to relate horizontal force on a boat to wind speed, and we now can relate drag on the hull to speed through the water, we can calculate the effective increase in wind speed that a tide will give. This is plotted below. No dependency on anchor type or scope etc, so I hope not controversial in principle.

I was surprised at how small an effect the tide has if aligned with the wind. My conclusion is that the undoubted effect of tide when at anchor is much more to do with the sheering, and thus dynamic forces it creates, than due to a simple increase in static load. Not exactly an earth-shattering conclusion.
The last thing I bothered plotting was the bollard pull I'd get, when motoring in reverse. This is less than the forward pull due to the different gear ratio, but in my case of a Gori not to do with propeller shape since it's symmetrical between forward and reverse.

It should tell me how many revs to apply when making sure my anchor is well dug in.
Working this out amused me for a few mins on a Friday lunchtime anyway. Have a good weekend.
