Question for the Astro-Navvies

[GHA]

Agree with these. It isn’t Rocket Science. For many, rote is the only way, hence why they think that a Template is a gift from Neptune. With a little more effort and coaching by Poseidon, figure out the basics of spherical trig and it becomes straightforward.

I've never actually got the hang of spherical trig, cartesian 2 dimensional makes sense with the sin etc just ratios but spherical... so lets have a look over morning coffee (need an excited emoji!)

So from memory the Admiralty AP3270 rapid sight reduction tables I have require 3 things, your Lat, the body Lat & difference in longs, LHA.

first stop perplexity> "Give an overview of the spherical trig involved in reducing a celestial sextant sight"

Answer
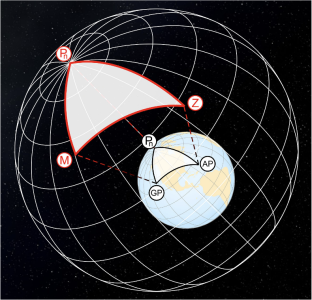
Celestial navigation using a sextant involves complex spherical trigonometry to convert the observed altitude of a celestial body into a position on Earth. The process, known as sight reduction, relies on solving the celestial navigation triangle, also called the PZX triangle
3
4
.

The PZX Triangle​

The PZX triangle is a spherical triangle formed on the celestial sphere by three points:

• P: The celestial pole (North or South)
• Z: The observer's zenith (directly overhead)
• X: The celestial body being observed (sun, star, planet, or moon)

The sides and angles of this triangle correspond to important navigational elements:

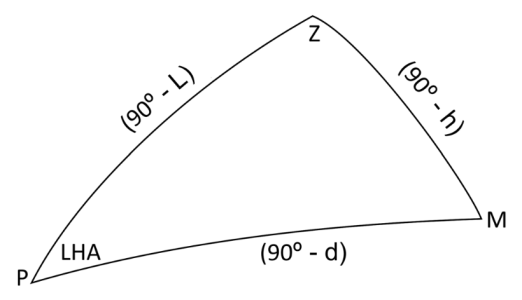
• PZ: Co-latitude (90° - latitude)
• PX: Co-declination (90° - declination of the celestial body)
• ZX: Co-altitude (90° - observed altitude)
• Angle at P: Local Hour Angle (LHA)
• Angle at Z: Azimuth
• Angle at X: Parallactic angle (not typically used in navigation)

So far so good, that makes sense, same angles just from a different datum.

Spherical Trigonometry Formulas​

The fundamental formula used in celestial navigation is the cosine formula for sides
3
cos⁡(a)=cos⁡(b)cos⁡(c)+sin⁡(b)sin⁡(c)cos⁡(A)cos(a)=cos(b)cos(c)+sin(b)sin(c)cos(A)

Where a, b, and c are the sides of the spherical triangle, and A is the angle opposite side a.

For the PZX triangle, this formula can be expressed as:
sin⁡(Ho)=sin⁡(Lat)sin⁡(Dec)+cos⁡(Lat)cos⁡(Dec)cos⁡(LHA)

Where:

• Ho is the observed altitude
• Lat is the observer's latitude
• Dec is the celestial body's declination
• LHA is the Local Hour Angle

Beyond me, can't visualise that so will just have to accept it, means remembering cos () no way could I figure that out from scratch. So "cosine formula for sides" sides means the angles if the GPs are extended to the centre of the earth?

Perplexity has access to Wolfram|Alpha Examples: Mathematics so should be able to do the sums.

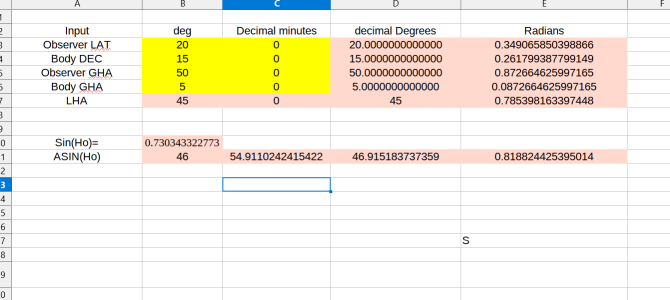
So picking one from ap3270..been a long while since this book was opened-

In the Rapid Sight Reduction Tables for Navigation (AP3270), LAT., LHA, and declination are key parameters used for celestial navigation calculations. Let's break down each of these terms:

LAT. (Latitude)​

LAT. refers to the assumed latitude of the observer's position on Earth. It is one of the primary arguments used to enter the sight reduction tables. In AP3270, latitude is typically given in whole degrees, ranging from 0° to 89° North or South
1
4
.

LHA (Local Hour Angle)​

LHA is the angle between the observer's meridian and the celestial body's hour circle, measured westward from 0° to 360°. It represents the apparent angular distance of the celestial body from the observer's meridian
2
. LHA is calculated by combining the Greenwich Hour Angle (GHA) of the celestial body with the observer's assumed longitude:

• For western longitudes: LHA = GHA - Longitude West
• For eastern longitudes: LHA = GHA + Longitude East

If the result exceeds 360°, subtract 360° to obtain the final LHA
2
.

Declination​

Declination is the angular distance of a celestial body north or south of the celestial equator, similar to latitude on Earth. In AP3270, declination is typically given in whole degrees, ranging from 0° to 29° North or South
1
4

Lets pick LAT =20º, Dec = 15º (same name as LAT), LHA = 45º.
Book says Hc = 46º 55'
So>
sin⁡(Ho)=sin⁡(Lat)sin⁡(Dec)+cos⁡(Lat)cos⁡(Dec)cos⁡(LHA)
sin⁡(Ho)=sin⁡(20)sin⁡(15)+cos⁡(20)cos⁡(15)cos⁡(45)
= 0.7303 from perplexity

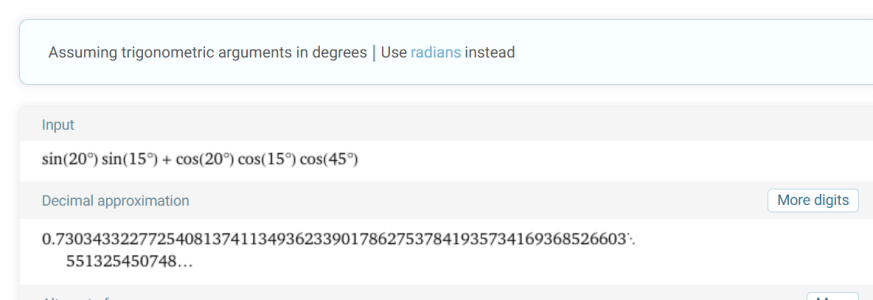
from .wolframalpha ^

So finally.... "what is arcsine(0.730343322772540813741134936233901786275378419357341693685266035513254507) in degrees and decimal minutes"

The arcsine of 0.730343322772540813741134936233901786275378419357341693685266035513254507 is approximately 46.7499999999999999999999999999999999999999999999999999999999999999999999°
or 46° 45'.

Close!!!! But should be closer, wonder why that is Still close enough to get the dopamine hit though
(Edit. Ask it to calc trig to 10 decimal degrees it comes up with 46° 54.91102')

Ah, wolframs
46.915183737359028075860755247167244855221419164415881621786507337574790225 degrees
0.915183737359028075860755247167244855221419164415881621786507337574790225*60 = 54.911024241541684551
46º54.91102424154168455'
YAY!!!!!!
Full dopamine!!!!

That must have been about 3 days in an astro nav classroom

 

[capnsensible]

Agree with these. It isn’t Rocket Science. For many, rote is the only way, hence why they think that a Template is a gift from Neptune. With a little more effort and coaching by Poseidon, figure out the basics of spherical trig and it becomes straightforward.

Well I don't know about those you have taught, but nearly all of my students aren't the slightest bit interested in the trigonometry. After a basic introduction they want to get in, take and reduce sights. Then plot them. Going through the tables and pro formas helps them understand the whys and wherefores. At the end they are competent and not bogged down with heavy theory. And they've all passed the Ocean exam where their understanding iof sight reduction s tested too.

You don't need to understand how an engine works to drive a car competently.

Mebbe it's because they are sailors first and not amateur mathematicians....

 

[GHA]

And 2nd coffee is enough time to bash out a quick spreadsheet.. which works!!

 

[Skylark]

Well I don't know about those you have taught, but nearly all of my students aren't the slightest bit interested in the trigonometry. After a basic introduction they want to get in, take and reduce sights. Then plot them. Going through the tables and pro formas helps them understand the whys and wherefores. At the end they are competent and not bogged down with heavy theory. And they've all passed the Ocean exam where their understanding iof sight reduction s tested too.

You don't need to understand how an engine works to drive a car competently.

Mebbe it's because they are sailors first and not amateur mathematicians....

My background is mechanical engineering and I'm conversing with GHA accordingly, and as a sailor. What happens in the classroom, stays in the classroom.

It isn't "one size fits all". Some people enjoy being stretched.

 

[Sandy]

Well I don't know about those you have taught, but nearly all of my students aren't the slightest bit interested in the trigonometry. After a basic introduction they want to get in, take and reduce sights. Then plot them. Going through the tables and pro formas helps them understand the whys and wherefores. At the end they are competent and not bogged down with heavy theory. And they've all passed the Ocean exam where their understanding iof sight reduction s tested too.

You don't need to understand how an engine works to drive a car competently.

Mebbe it's because they are sailors first and not amateur mathematicians....

Well said.

 

[GHA]

My background is mechanical engineering and I'm conversing with GHA accordingly, and as a sailor. What happens in the classroom, stays in the classroom.

It isn't "one size fits all". Some people enjoy being stretched.

Well, everyone is different.
Just learning how to copy numbers from a book without getting a feel for the real universe seems like a waste of time imho, why not just download an app Slide rules & logs went in the bin decades ago as better methods came along.

But many seem happy enough just to blindly follow a method without understanding it so down to them.

Though generally people *are* actually interested afterwards down the bar to dig a bit deeper anything.

And it's just textbook conformation bias at the end of the day, so many are incapable of not reacting to the idea that there may be other ways to look at things just as valid as what they assume to be some kind of external reality.

Watch now for the fireworks, bye bye thread

on social media sometimes people get annoyed and lash out if anyone suggests a different point of view to theirs - is this a scientifically studied human trait?​

Answer
Yes, the tendency for people to react negatively to differing viewpoints on social media is a scientifically studied human trait. This behavior is rooted in several psychological and social phenomena that researchers have investigated.

Negativity Bias and Online Behavior​

Research has shown that negativity tends to drive online behavior more than positivity. A study published in Nature Human Behaviour found that negative language in online content is linked to higher user engagement
4
. This negativity bias extends to how people react to opposing viewpoints, often leading to more intense and hostile responses.

Social Comparison and Emotional Responses​

Social media creates an environment ripe for social comparison, which can lead to negative emotional responses. A meta-analysis of 48 studies revealed that exposure to upward social comparisons on social media (comparing oneself to those perceived as better off) results in negative self-evaluations and emotions
1
. This heightened emotional state can make users more prone to lashing out when confronted with differing opinions.

Confirmation Bias and Echo Chambers​

People tend to seek out information that confirms their existing beliefs, a phenomenon known as confirmation bias. Dr. Michael Workman's study found that when individuals have already formed an opinion on a topic, they are less likely to change their minds based on social media interactions
5
. This tendency can lead to the formation of echo chambers, where users are exposed primarily to views that align with their own, making encounters with differing opinions more jarring and potentially leading to hostile reactions.

Anonymity and Disinhibition​

The sense of anonymity or distance provided by social media platforms can lead to what psychologists call the online disinhibition effect. This effect can cause people to behave in ways they wouldn't in face-to-face interactions, including being more aggressive or confrontational when faced with opposing viewpoints
9
.

Emotional Responses and Mental Health​

Research has shown that emotional responses to social media experiences are linked to mental health outcomes. A study of adolescents found that negative emotional responses to social media experiences were associated with higher levels of depressive symptoms
7
. This emotional volatility can contribute to more reactive and aggressive behavior when encountering differing opinions.

Personality Traits and Online Behavior​

Individual personality traits play a role in how people behave on social media. Studies have found correlations between personality traits (such as the Big Five model) and online behavior, including how people respond to differing viewpoints
8
. Some individuals may be more prone to aggressive reactions based on their personality characteristics.In conclusion, the tendency for people to react negatively to differing viewpoints on social media is indeed a scientifically studied human trait. It stems from a combination of psychological biases, social comparison processes, the nature of online interactions, and individual personality factors. Understanding these underlying mechanisms can help in developing strategies to promote more constructive online discussions and mitigate the negative effects of social media interactions.

 

[S04]

So finally.... "what is arcsine(0.730343322772540813741134936233901786275378419357341693685266035513254507) in degrees and decimal minutes"

The arcsine of 0.730343322772540813741134936233901786275378419357341693685266035513254507 is approximately 46.7499999999999999999999999999999999999999999999999999999999999999999999°
or 46° 45'.

The result of that calculation is nonsense so whatever magic tool rendered it is suspect. Just using 5 DP, arcsine(0.73034) is 0.81882 radians = 46.91488° =46° 54.9'

 

[Skylark]

Well, everyone is different.


Watch now for the fireworks, bye bye thread

Agreed, I was enjoying the banter but along came the size 12 boots with the high and mighty attitude “I know best and only my view is right” pouring cold water on to it.

Buon Natale.

 

[GHA]

The result of that calculation is nonsense so whatever magic tool rendered it is suspect. Just using 5 DP, arcsine(0.73034) is 0.81882 radians = 46.91488° =46° 54.9'

must have been a typo from me, less resolution is indeed quite close
You`re calling wolframalpha some magic tool

 

[GHA]

Agreed, I was enjoying the banter but along came the size 12 boots with the high and mighty attitude “I know best and only my view is right” pouring cold water on to it.

Buon Natale.

Actually thought about a thread on just how dangerous rampant conformation and the plethora of other human biases every human suffers from is on a sailing boat but seems no point at all on here, question everything including (or more so) what you don't question
Anyway, it's been an interesting thread & good motivation to dig deeper.

Though lets be honest, irrelevant to sailing other than a fun ancient practice.

Just updated the long passage check list to include charging a couple of the old mobile phones & sticking in a faraday cage. GPS won't go down but lightning can strike..

 

[S04]

You`re calling wolframalpha some magic tool

No, the "magic tool" was whatever gave that incorrect answer. You've now confirmed it wasn't Wolfram.

 

[requiem]

So from memory the Admiralty AP3270 rapid sight reduction tables I have require 3 things, your Lat, the body Lat & difference in longs, LHA.
...
Lets pick LAT =20º, Dec = 15º (same name as LAT), LHA = 45º.
Book says Hc = 46º 55'
So>
sin⁡(Ho)=sin⁡(Lat)sin⁡(Dec)+cos⁡(Lat)cos⁡(Dec)cos⁡(LHA)
sin⁡(Ho)=sin⁡(20)sin⁡(15)+cos⁡(20)cos⁡(15)cos⁡(45)

It also helps to have a triangle involved. If you have a melon or other round object handy that you're willing to mark up, use a pen to mark the sides of the "triangle" on it and let us know what you find.

 

[GHA]

No, the "magic tool" was whatever gave that incorrect answer. You've now confirmed it wasn't Wolfram.

Perplexity has full access to Wolfram, you can watch it forming prompts & having a chat as it compiles the response . Often for questions not involving any sums.
Also has access to

GPT-4 Omni: This is OpenAI's latest model for ChatGPT, known for its strong reasoning abilities and versatility across multiple tasks5.
Claude 3.5 Sonnet and Haiku: These are Anthropic's latest releases, with Claude 3.5 Sonnet being particularly adept at handling nuanced language tasks5.
Llama 3: Perplexity Pro includes access to a 32k token version of Llama 3 70b6.
Perplexity's own models: This includes their default model optimized for speed and web browsing, as well as their experimental models5.
DALL-E 3 and Stable Diffusion XL:
These are image generation models that give Perplexity multimodal capabilities

Valued a $9billion it ain't no magic tool, but quite scarily powerful..

I've started putting the log in from passages & asking for an NLP analysis
To head those biases off you need to admit they are there first.....

 

[GHA]

It also helps to have a triangle involved. If you have a melon or other round object handy that you're willing to mark up, use a pen to mark the sides of the "triangle" on it and let us know what you find.

Got a melon in my head Actually was looking at the moon & sun earlier & it's breath taking visualising just the scale of what's going on

 

[S04]

Got a melon in my head

I've a brain in mine but as you say, everyone is different.


Oops, nearly forgot to add the seeming necessary emoji

 

[Frank Holden]

For those that want true in depth understanding I suggest reading and inwardly digesting all of this Spherical trigonometry - Wikipedia
There is a bit more about John Napier and his rules here Napier’s Nifty Rules

For those - such as the OP - who simply want to become competent navigators I offer this -

Celestial navigation involves - in most cases - the solving of a spherical trigonometry problem.
While plane trigonometry - which most of us learnt at school - involves using two parts to find a third spherical trigonometry involves using three parts to find a fourth. These four parts are the Local Hour Angle ( the angle at the pole ) , the Co-Lat, the Co-Dec, and the Zenith Distance.
The problem can be resolved by either using the Haversine Formula and Logarithms or by using the Air Navigation Tables.

That did not take three days to explain as someone suggested but a mere 35 seconds.

Moving right along - how to establish the Hour Angle ..........

 

[requiem]

Ah, I missed that your formula was converted to take the latitude and declination directly, rather than using "90°-x". Here's your triangle, no need to extend the GPs to earth's center here. It looks like the classic "side-angle-side" from school, now on a curved surface:



With the basic law of cosines being "cos a = cos b cos c + sin b sin c cos A", if you don't want to use the co-latitude, co-declination directly, you can multiple cos(A) with the cos(b) cos(c) bit of multiplying it by the sin(b) sin(c) bit.

I'm very likely to make some mistakes here, but working it out helps me learn too...

Assume LHA of 30°, Lat of 10°N, dec of 15°S, formula "sin h = sin L sin d + cos L cos d cos LHA":

sin h = sin(10°) sin(-15°) + cos(10°) cos(-15°) cos(30°)​

sin h = -sin(10°) sin(15°) + cos(10°) cos(-15°) cos(30°) (edit: found the error!)​

sin h = -0.8688 0.77886​

h = -60.3138, or... 60° 18.8'​

h = 51.1567078°, and indeed 90° less that is 38.8432922​

Doing a quick sanity check, the actual distance should be closer to 39°, but here the zenith distance is 90°-h or 29.6862°.

Are the negative values already causing trouble? Let me see... running again with a dec of 15°N, the numbers come out the same. But, a 5° difference in latitude should result in a much shorter distance compared to a 25° difference, all else being equal. Going back to the basic formula...

cos a = cos b cos c + sin b sin c cos A​

cos(zd) = cos(80°) cos (105°) + sin(80°) sin(105°) cos(30°)​

cos(zd) = -0.04494 + 0.82381​

cos(zd) = 0.77886​

zd = 38.8437 (This is better!)​

Avoiding negatives when working with log tables is where the ha'versine is supposed to come into play. Digging up an old textbook...



Note that as the angle increases, the versed sine or versine will increase until it represents the full diameter of the circle, declining back to zero as the angle increases to the full 360°. This means it spans from 0 to 2, and taking half of it gives you values spanning from 0 to 1 for all angles.

Since the versine is 1-cos(θ), and the ha'versine is 1/2(1-cos(θ)) you can go:

hav(θ) = 1/2 ( 1 - cos(θ) )​

2 hav(θ) = 1 - cos(θ)​

cos(θ) = 1 − 2 hav(θ)​

and with a bit more re-arrangement thanks to Wikipedia you eventually end up with..

hav(c) = hav( a - b ) + sin(a) sin(b) hav(C), or...​

hav(h) = hav( co-Lat - co-dec ) + sin(co-Lat) sin(co-dec) hav(GHA)​

Hopefully that's mostly right; I think I've an old set of tables somewhere...

 

[Frank Holden]

and with a bit more re-arrangement thanks to Wikipedia you eventually end up with..

hav(c) = hav( a - b ) + sin(a) sin(b) hav(C), or...​

hav(h) = hav( co-Lat - co-dec ) + sin(co-Lat) sin(co-dec) hav(GHA)​

Hopefully that's mostly right; I think I've an old set of tables somewhere...

And then you can simplify that by replacing sin(co-Lat) and sin (co-Dec) with cos(Lat) and Cos (Dec) and simply use hav( lat ~dec) .
Bingo! haversine formula.

I've just dug out Mike Harris's 'Astronavigation by Pocket Computer.
The formula he used for programming in Basic was the Cosine formula.
( SIN LAT x SIN DEC ) + ( COS LAT x COS DEC x COS LHA)
Once again lets you get rid of the CoLat and CoDec bit as required if you use the Sine formula..


In 1990 I used an article of his published in PBO to program a Sharp PC1246 which was cutting edge at the time.

 

[requiem]

Indeed, and in working this out I found the error in my previous post, so everything comes together nicely, with some minor differences likely due to rounding. (I used Wolfram to check, since it has the haversine functions.)

 

[Skylark]

Enjoying the thread.

Interesting that Bowditch uses air tables / intercept method and doesn't describe the Haversine method as an alternative (my copy is 2002 Bicentennial Edition).

I've been Googling, trying to keep up with some of the very knowledgeable posters on here, and come across Bygrave Slide Rule.

http://tinas-sliderules.me.uk/Slide Rules/Tina's Bygrave.pdf