Probability of being in a Cocked Hat

[Bi111ion]

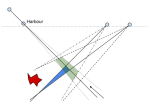
I think the point of all this is that you could be closer than the nearest corner. It's made me more thankful for GPS.

Yes that is the point.

Of course the principle applies to GNSS such as GPS. Fortunately you typically have a lot of satellites in view under normal conditions at sea. The probability contours are still ellipses, but with enough sats and enough averaging they tend to be close to circular and so the reported error in metres is a pretty good guide. If the GNSS signals were being jammed or spoofed, but you were able to get a few reliable signals but at unfavourable angles the same principle would hold. Each pair of sats gives you a hyperboloid of position but on a small scale this looks like a line (just as in celestial navigation a LOP is really part of a circle).

 

[TLouth7]

I'm not convinced that the size or shape of a cocked hat tells us any information about the probability distribution of our position. We can say that the best estimate of position (fix/MLP) necessarily falls within the cocked hat, but otherwise it is not a good guide. Having the long axis of the probability ellipse parallel to the longest side of the triangle implies that we place more weight on the two nearly parallel fixes, but is this fair? A more robust approach would be to draw confidence intervals on each position line and find the polygon that falls within these.

Consider the hypothetical case where I am following leading marks towards a harbour. In order to find out how far along the track I am I take bearings to an adjacent pair of landmarks on the coast. Plotting this gives me the following chart section, with cocked hat in blue and confidence polygon in green:



Using the "worst case scenario" approach I would put my EP at the leftmost tip of the cocked hat and take evasive action for the large (red) rock, but is that really necessary?

 

[Sandy]

We can say that the best estimate of position (EP) necessarily falls within the cocked hat

We need to be careful about the us of words here.

My understanding of an Estimated Position is quite different to that. An EP is an extension of a dead reckoning, where you only use course and speed, and add the tide's set and drift, it is for use offshore. A cocked hat is a three point fix.

 

[TLouth7]

We need to be careful about the us of words here.

Quite right, I have edited my comment.

 

[Bi111ion]

I'm not convinced that the size or shape of a cocked hat tells us any information about the probability distribution of our position. We can say that the best estimate of position (EP) necessarily falls within the cocked hat, but otherwise it is not a good guide. Having the long axis of the probability ellipse parallel to the longest side of the triangle implies that we place more weight on the two nearly parallel fixes, but is this fair? A more robust approach would be to draw confidence intervals on each position line and find the polygon that falls within these.

Consider the hypothetical case where I am following leading marks towards a harbour. In order to find out how far along the track I am I take bearings to an adjacent pair of landmarks on the coast. Plotting this gives me the following chart section, with cocked hat in blue and confidence polygon in green:

View attachment 79803

Using the "worst case scenario" approach I would put my EP at the leftmost tip of the cocked hat and take evasive action for the large (red) rock, but is that really necessary?

So first of all your point "I'm not convinced that the size or shape of a cocked hat tells us any information about the probability distribution of our position.". Well it tells us several useful things. First of all assuming the variances of the errors are known and Gaussian it gives us the maximum likelihood position (the symmedian point, or weighted symmedian point for different variances), if not Gaussian it is the best unbiased linear estimate. Secondly if you assume the errors are Gaussian you can draw the elliptical probability contours for a given probability based on the triangle (as in my paper)

(I am assuming the land marks are distant here, your chart-let is probably not to scale! Under this assumption the errors give approximate parallel translates of LOPs)

You write "We can say that the best estimate of position (EP) necessarily falls within the cocked hat," Yes the (weighted) symmedian point always lies within the cocked hat. If we know the variances (weights) we can find where it is in the cocked hat (see examples in the paper). The point is if the variances are equal it will be closest to the shortest side. In fact the distance to each line of position are in the same proportion as the lengths of the sides of the cocked hat (these are the "trilinear coordinates")

In your example illustrated, the error bars you draw on the two bearings to land marks are about twice as big as the error on the bearing to the harbour leading marks. That means we trust those LOPS less and it moves the weighted symmedian even closer to the LOP for the harbour leading marks. This is what you would think intuitively. It makes the probability ellipse less skinny than it would normally be for such an acute triangle. As mentioned in the paper there is some choice of variances that makes it a circle (say if you have the possibility of averaging more bearings or simply trying harder to get an accurate bearing).

"confidence polygon in green:" I think this assumes a uniform distribution of errors, so it is equally likely to be anywhere within the error bars. But it is easy to draw and a good guide.

 

[Bi111ion]

Quite right, I have edited my comment.

In the navigation literature I have seen "most likely position" MLP. In statistics it would be called the maximum likelihood estimate of the position. As said above we should keep EP for DR + tide and leeway.

 

[maxi77]

We need to be careful about the us of words here.

My understanding of an Estimated Position is quite different to that. An EP is an extension of a dead reckoning, where you only use course and speed, and add the tide's set and drift, it is for use offshore. A cocked hat is a three point fix.

Indeed a fix is taken to refine the EP and it's associated pool of errors.

 

[TLouth7]

So first of all your point "I'm not convinced that the size or shape of a cocked hat tells us any information about the probability distribution of our position.". Well it tells us several useful things. First of all assuming the variances of the errors are known and Gaussian it gives us the maximum likelihood position (the symmedian point, or weighted symmedian point for different variances), if not Gaussian it is the best unbiased linear estimate. Secondly if you assume the errors are Gaussian you can draw the elliptical probability contours for a given probability based on the triangle (as in my paper)

I agree with the use of symmedian point for MLP (with bias for confidence in each LoP), though I don't suppose anyone is going to construct it in reality. The problem with probability ellipse is that at its limit where two bearings approach each other what you in effect have is a 2-point fix. Because the cocked hat would be long and thin the ellipse would be too, whereas a 2-point fix would give a circle. This comes about because you are giving double weight to the adjacent bearings compared to the perpendicular one, but is this valid? You could take one bearing from each of two adjacent objects, and two from one at right-angles and end up with a 4-point fix giving a circle despite having no new information.

(I am assuming the land marks are distant here, your chart-let is probably not to scale! Under this assumption the errors give approximate parallel translates of LOPs)

The only time the objects could be considered distant is celestial nav. For any bearing to a physical object clearly the error is in the angle. If I were bothered to draw this it would be as per my diagram, first draw the bearing and then some sort of limit lines (e.g. ±5°). I agree that mathematically these could be treated as parallel but for construction on a chart they are not.

"confidence polygon in green:" I think this assumes a uniform distribution of errors, so it is equally likely to be anywhere within the error bars. But it is easy to draw and a good guide.

The appeal of the confidence polygon over the cocked hat is that it gives an estimate of the area you could be in that is based on the precision of the measurements rather than on a single random event, while being much easier to construct than the actual density function (ellipse family).

 

[Bi111ion]

The problem with probability ellipse is that at its limit where two bearings approach each other what you in effect have is a 2-point fix. Because the cocked hat would be long and thin the ellipse would be too, whereas a 2-point fix would give a circle.

The probability contour for a two line fix is still an ellipse assuming equal variances and the LOPS not meeting at 90 degrees. The paper on DF I refer to in my paper Stansfield, R. (1947), illustrates this also.

Because the cocked hat would be long and thin the ellipse would be too, whereas a 2-point fix would give a circle.

Stansfield also explains why for distant objects you can consider the error as a parallel translation even for bearings. I think perhaps if they are close enough for this not to work you either have very big errors in the bearing or you are close enough to see where you are.

The appeal of the confidence polygon over the cocked hat is that it gives an estimate of the area you could be in that is based on the precision of the measurements rather than on a single random event, while being much easier to construct than the actual density function (ellipse family).

Right. The point is if you don't have a good estimate of the errors in the LOPS all you get from the cocked hat is the residual squared error, and while this provides an unbiased estimate for the variance of the bearings it is a very poor estimate as there is only one extra line (so one more equation than variables). The cocked hat tells you what shape the ellipse is and which way it points (assuming equal errors) but it does not give a good idea of how big it is.

So folks don't have to scroll back here is the link to the JoN article again or if that doesn't work for you preprint pdf version .

Stansfield's paper is on 10.1049/ji-3a-2.1947.0087 but I am not sure if it is paywalled.

The old French book Yvon-Villarceau, A. J. F. & Aved de Magnac, H. J. (1877) I found was online (indeed a link to it in NavList discussion http://fer3.com/arc/m2.aspx/Villarceau-Nouvelle-navigation-astronomique-AndrésRuiz-jul-2017-g39399)

 

[TLouth7]

The probability contour for a two line fix is still an ellipse assuming equal variances and the LOPS not meeting at 90 degrees. The paper on DF I refer to in my paper Stansfield, R. (1947), illustrates this also.

I think this supports my point that the cocked hat is not inherently relevant to the probability density. It is perfectly possible to construct a family of ellipses for a 2-point fix, and it would also be possible for a 3-point fix that just happened to cross perfectly. All the information you need is in the Lines of Position, and the cocked hat is just a random statistical artifact. I don't deny that it would be useful for constructing the ellipses, or that it can act as a visual guide to the shape of the distribution.

Stansfield also explains why for distant objects you can consider the error as a parallel translation even for bearings. I think perhaps if they are close enough for this not to work you either have very big errors in the bearing or you are close enough to see where you are.

Sure, but if I am taking bearings with a compass then my error is going to be an angle, independent of distance to the object. To turn that error into a distance I have to multiply angle (in radians) by distance off, which seems to be an extra, unnecessary step.

The point is if you don't have a good estimate of the errors in the LOPS all you get from the cocked hat is the residual squared error, and while this provides an unbiased estimate for the variance of the bearings it is a very poor estimate as there is only one extra line (so one more equation than variables). The cocked hat tells you what shape the ellipse is and which way it points (assuming equal errors) but it does not give a good idea of how big it is.

I agree fully with this. If you are good at taking bearings/sights then you should expect to see small cocked hats, but if for a particular fix you get a small cocked hat it doesn't mean your bearings were good.

Stansfield's paper is on 10.1049/ji-3a-2.1947.0087 but I am not sure if it is paywalled.

It does seem to be.

 

[Bi111ion]

This is Fig 2 from R.G. Stansfield, Statistical theory of d.f. fixing , Journal of the Institution of Electrical Engineers - Part IIIA: Radiocommunication 1947, 762 - 770 It illustrates the elliptical contours from a two line fix (to distant objects) for a range of angles between the LOPs. It seems you have to pay for the full article https://digital-library.theiet.org/content/journals/10.1049/ji-3a-2.1947.0087 even though it is a very old paper.

 

[Bi111ion]

I made a little Geogebra app that you can change the triangle and the weights to see where the weighted symmedian goes . Use the arrow tool to drag around the corners of the cocked hat A B or C and then change the sliders to change the standard deviation for each Line of Position

https://www.geogebra.org/classic/mrguw2kx

 

[lw395]

I'm not convinced that the size or shape of a cocked hat tells us any information about the probability distribution of our position. We can say that the best estimate of position (fix/MLP) necessarily falls within the cocked hat, but otherwise it is not a good guide. Having the long axis of the probability ellipse parallel to the longest side of the triangle implies that we place more weight on the two nearly parallel fixes, but is this fair? A more robust approach would be to draw confidence intervals on each position line and find the polygon that falls within these.

Consider the hypothetical case where I am following leading marks towards a harbour. In order to find out how far along the track I am I take bearings to an adjacent pair of landmarks on the coast. Plotting this gives me the following chart section, with cocked hat in blue and confidence polygon in green:

View attachment 79803

Using the "worst case scenario" approach I would put my EP at the leftmost tip of the cocked hat and take evasive action for the large (red) rock, but is that really necessary?

If you think you are on a transit, either you are on that transit or you are mistaking the transit lights/marks and you know jack shit.
It's not any kind of pretentious distribution.

Normally you'd confirm the transit with a compass reading, but it's easy for people to find e.g. two white objects convincingly near enough the transit bearing.

 

[Amulet]

The theoretical aspect of this is much fun - for me too. When on a boat bouncing around in the dark the detail might be lost. I have noticed that the inexperienced can latch on to rules of thumb heard under instruction, like "assume you are at the corner of the cocked-hat nearest to danger." You should be concerned about where you could be, and you easily could be a lot closer to danger than that. It is a bad rule of thumb (without qualification). I'm not sure whether there is a rule of thumb that could replace it, but if there is some of the contributors to this thread could perhaps formulate it.

I'm anxious enough to assume that if I'm near rocks my boat is actively trying to hit them, and that I have to strive to miss them by huge margins.

 

[Amulet]

I'm not convinced that the size or shape of a cocked hat tells us any information about the probability distribution of our position. We can say that the best estimate of position (fix/MLP) necessarily falls within the cocked hat, but otherwise it is not a good guide. Having the long axis of the probability ellipse parallel to the longest side of the triangle implies that we place more weight on the two nearly parallel fixes, but is this fair? A more robust approach would be to draw confidence intervals on each position line and find the polygon that falls within these.

Consider the hypothetical case where I am following leading marks towards a harbour. In order to find out how far along the track I am I take bearings to an adjacent pair of landmarks on the coast. Plotting this gives me the following chart section, with cocked hat in blue and confidence polygon in green:

View attachment 79803

Using the "worst case scenario" approach I would put my EP at the leftmost tip of the cocked hat and take evasive action for the large (red) rock, but is that really necessary?

It would be necessary on my boat. You only need to have made a pig's ear of one bearing to be in big trouble. I'd be taking evasive action and looking for extra evidence on position - depth, or maybe another bearing. (Of course two of your bearings are so close that it scarcely qualifies as a three pint fix - maybe a two and a half point fix, if that.) .... typo, but I like the concept of a three pint fix., which it might be.

 

[lw395]

The theoretical aspect of this is much fun - for me too. When on a boat bouncing around in the dark the detail is might be lost. I have noticed that the inexperienced can latch on to rules of thumb heard under instruction, like "assume you are at the corner of the cocked-hat nearest to danger." You should be concerned about where you could be, and you easily could be a lot closer to danger than that. It is a bad rule of thumb (without qualification). I'm not sure whether there is a rule of thumb that could replace it, but if there is some of the contributors to this thread could perhaps formulate it.

I'm anxious enough to assume that if I'm near rocks my boat is actively trying to hit them, and that I have to strive to miss them by huge margins.

A first step to understanding what your cocked hat is actually telling you is to get out there and plot lots of cocked hats and see how they stack up against reality.
But if you are comfortably producing credible fixes on sunny days, be aware that when the wheels start coming off and you're trying to take bearings in the rain in F6, the accuracy will be less 'textbook'.
The prudent pilotage operator adopts strategies that allows his bearings to be dog rough and still keep him safe.

I recall a conversation, the Bowdlerised version goes something like:
Where are we?
We're Ok, we're in 25m of water.

In real-life 'getting into port' escapades, how often is the cocked hat academic conundrum actually relevant?
Mostly we are relatively sure about one position line and a bit more vague in the other dimension? Or we are sure that we are one side of a transit, or outside a contour.

Plotting cocked hats and wondering about the standard deviation for error is pretty much just something to do when you're in the middle of an ocean with nothing to hit and time on your hands.
Coastal 'yottigation' is not about knowing where you are within a 95% confidence contour, it's about being damned sure you're on the safe side of the line.

 

[Bi111ion]

In real-life 'getting into port' escapades, how often is the cocked hat academic conundrum actually relevant?
Mostly we are relatively sure about one position line and a bit more vague in the other dimension? Or we are sure that we are one side of a transit, or outside a contour..

Absolutely My first coastal navigation making serious passage was on a OYC ketch from Liverpool to Hamble in the 1970s as "third mate". I worked up EPs, took bearings on whatever I could see but what kept me feeling safe was the depth sounder and being outside a safe contour. Every now and again the skipper would pop up on deck, look around, look at my chart work, switch on the radar to see where we really were and go back down. He didn't say anything so I assumed I was close enough.

I have always been very suspicious of hand bearings and on coastal passages in the UK transits and opening angles eg on headlands give really good evidence that you are on one side of a line. I think navigators are always evaluating evidence, checking it is consistent and keeping mental error bars in their head.

 

[maxi77]

A very interesting thread with some maths that makes my brian hurt( that was deliberate and refers to the morning I stumbled into the radar office as we slipped to find my plotter slumped in the corner with 'My Brian hurts' written in chinagraph on the radar screen. I did my blind pilotage work on my own that morning). I think though that in some respects we are drifting away from the real problem which is how do we avoid bumping into bits of land. If you are several days from land fall an error of 50 miles whilst it may not be that professional still will not really cause you any severe problems, going up the Clyde it would be a different thing. The real question is do we understand the accuracies of the systems we use and do we allow for this in our plotting. If one takes an astro fix, the good guys will probably hit a 1 mile CEP on average, I would rate myself nearest 5 miles, and on a yacht deck in bad weather. who knows. This is one of the reasons we tend not to use astro in coastal waters if it can be avoided. For visual fixes we expect better but we still have to rate just how accurate the raw data is, related to just how much accuracy we need and when we decide we do not have enough accuracy to do the passage safely then it is time to stop. When fixing with a handbearing compass I tend to rate each bearing and use that to help resolve the cocked hat and if safety is a problem act accordingly which may be paying more attention to the sounder or steering out a bit from the point of danger

 

[mattonthesea]

The real question is do we understand the accuracies of the systems we use and do we allow for this in our plotting.

If I have any doubt about the safety aspect of my accuracy in fixes then I look for evidence that may suggest that I am wrong. EG: an/that object should/should not be there; the depth does not correlate.

 

[Bi111ion]

Interestingly the discussion of cocked hats still continues, not just in pubs but also in the Journal of Navigation.

George Kaplan recently published this paper in which he does a simulation to find probabilities
Kaplan GH, Fix Probabilities from LOP Geometry DOI: Fix Probabilities from LOP Geometry | The Journal of Navigation | Cambridge Core

Robin Stuart managed to integrate normal distributions over triangles giving an explicit answer for the probabilities of being in a given cocked hat (rather than a random one), that is the paper I mentioned at the start of this thread
Stuart, RG. Probabilities in a Gaussian cocked hat. DOI: Probabilities in a Gaussian Cocked Hat | The Journal of Navigation | Cambridge Core

My own contribution is for people who really like ruler and compass constructions! (If you dont like that kind of old school Geometry you will not like the paper, but I really enjoyed the geometry of the horizontal sextant angle fix when I learnt it as a kid, and that obviously affected me!)
Lionheart, William RB, Peter JC Moses, and Clark Kimberling. The Geometry of Elliptical Probability Contours for a Fix using Multiple Lines of Position. DOI: The Geometry of Elliptical Probability Contours for a Fix using Multiple Lines of Position | The Journal of Navigation | Cambridge Core

I also made some (pretty bad) YouTube videos of me doing the construction for the probability ellipse. Demonstrating I think that while it is possible even dedicated scientifically trained naval officers in the age of sail would not have been bothered to construct an elliptical probability contour at sea unless it involved a bet with a barrel of rum as the stakes. I wonder if some secret archives of the Napoleonic navy would reveal they actually knew of this technique though and it was a military secret? Navigation and Geometry

A new paper has just come out in preprint
Bárány, Imre, William Steiger, and Sivan Toledo. "The cocked hat." arXiv preprint [2007.06838] The cocked hat
They consider the case where the LOPs are bearings, so "rays" not lines. So if you were really bad at taking bearings you could be on the wrong side of the landmark. Interestingly, with very general assumptions very carefully stated they still come out with 1/4.

I suppose I should not just cock but doff my hat to them!